こちらの記事で、時系列データを簡単に可視化する方法を紹介しました。
なので今回は金融チャートに必ず用意されている移動平均線を計算し、追加する方法を紹介します。
時系列データも同じサイトにアップしたデータを使っているので、リンク先からダウンロードすれば自由に活用いただけます。
完成イメージ
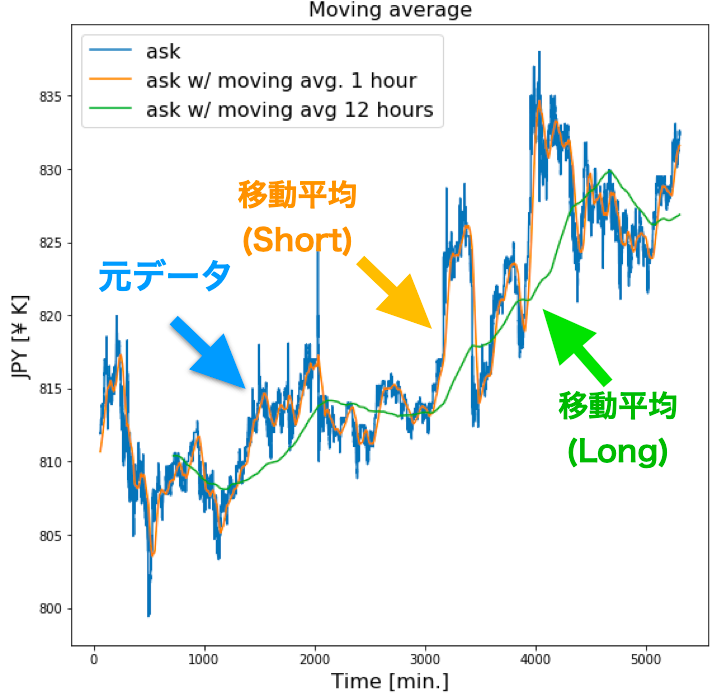
オリジナルの時系列データと2つの移動平均線Short, Longを計算し、同時に描画しています。
移動平均について詳しく知りたい方は、統計Webの説明が分かりやすかったので参考にしてください。
移動平均線の求め方
pythonを使って移動平均を計算する手順は次の通りです。
- 移動平均のサイズを決める
- 畳み込み演算にて移動平均を計算する
それでは順番に紹介していきます。
移動平均のサイズを決める
移動平均のサイズによって平均を取る期間が決まります。
移動平均のサイズを変えたい場合は、このパラメータで調整できます。
今回は期間を1時間と、12時間とした2つの移動平均線を求めていきます。
s_filter_1 = 1 * 1200 # 移動平均のサイズ 。 1200で1時間です。
s_filter_2 = 12 * 1200 # 移動平均のサイズ(12時間)
畳み込み演算にて移動平均を計算する
移動平均線は、先ほど設定した移動平均のサイズを持つフィルタを畳み込み演算することで求まります。
pythonでは畳み込み演算を行う関数np.convolveが用意されているので、それを使えば簡単に移動平均を計算できます。
np.convolve関数を使った移動平均線の計算
filter = np.ones(s_filter) / s_filter # 平均を計算するフィルタサイズ
np.convolve(data, filter, mode='full')
# data: 時系列データ
移動平均線を重ねたグラフを作成
では実際に2つの移動平均線を計算していきます。
s_filter_1 = int(1 * 3600 / data_span) #移動平均線用のfilterサイズ(1時間)
s_filter_2 = int(12 * 3600 / data_span) # 移動平均線用のfilterサイズ(12時間)
# 移動平均のfilterを生成
slide_filter_1 = np.ones(s_filter_1) / s_filter_1
slide_filter_2 = np.ones(s_filter_2) / s_filter_2
# 横軸の上限値を設定
x_range = xx.shape[0]
# 畳み込み演算による移動平均線の生成
ask_mavg_1 = np.convolve(df_data['ask'], slide_filter_1, mode='full') # 移動平均(1時間)
ask_mavg_2 = np.convolve(df_data['ask'], slide_filter_2, mode='full') # 移動平均(12時間)
移動平均線を計算したので、グラフにしていきます。
fig, ax = plt.subplots(figsize = (9,9))
ax.plot(xx[s_filter_1:] / 60, df_data['ask'][s_filter_1:] / 1000, label='ask')
ax.plot(xx[s_filter_1:] / 60, ask_mavg_1[s_filter_1:x_range] / 1000 ,label='ask w/ moving avg. 1 hour')
ax.plot(xx[s_filter_2:] / 60, ask_mavg_2[s_filter_2:x_range] / 1000 ,label='ask w/ moving avg 12 hours')
ax.legend(fontsize=16)
ax.set_xlabel('Time [min.]', fontsize=16)
ax.set_ylabel('JPY [¥ K]', fontsize=16)
ax.set_title('Moving average', fontsize=16)
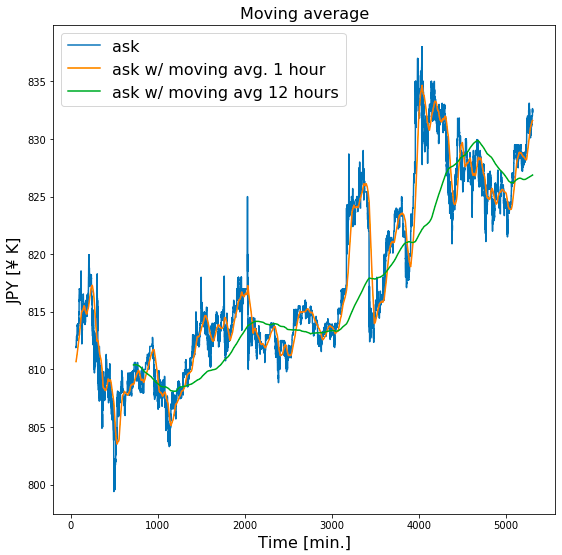
青の線がオリジナルの時系列データ、オレンジの線が移動平均サイズを1時間とした移動平均線、緑の線が移動平均サイズを12時間とした移動平均線です。
オレンジの線はオリジナルデータを滑らかにしつつも、全体的な形は捉えています。
一方、緑の線はオレンジの線よりもさらに滑らかになっており、オリジナルの時系列データの変化にゆっくり付いていっています。
これは移動平均がローパスフィルタといって、変化の早い高周波成分を除去する働きがあるためです。そのため短期間でのノイズのような変化を除外して分析するのに役立ちます。
(おまけ)移動平均線と金融チャート
移動平均線は株価や為替といった金融チャートで頻繁に用いられています。
それは短時間での変動が激しい金融チャートの特徴を分析するのに移動平均線が優れているからです。
ここでは、おまけとして移動平均線に関連する金融用語を少しだけ紹介し締めたいと思います。
- ゴールデンクロス
短期間の移動平均線が長期間の移動平均線を下から上に交差すること。
金融チャートが上昇するサインと言われています。 - デッドクロス
ゴールデンクロスとは逆に、短期間の移動平均線が長期間の移動平均線を上から下に交差すること。
金融チャートが下降するサインと言われています。 - 参考:ゴールデンクロスとデットクロス【初心者向け株投資入門】


コメント