numpy.convolveを使って移動平均を計算
1次元の畳み込み演算を行うnumpy.convolveを利用して移動平均を計算します。
numpy.convolveの仕様
公式リファレンスの内容をまとめました。
modeによって出力に違いがあるので、詳しい説明について後述します。
numpy.convolve(a, v, mode='full')
概要
配列のような1次元系列を2つ入力し、畳み込み結果を返す。
| パラメータ | 型 | 説明 |
|---|---|---|
| a | array_like[長さN] | 1次元のアレイ |
| v | array_like[長さM] | 1次元のアレイ |
| mode | 'full', 'same', 'valid' | (省略可)標準では'full' 畳み込み演算の出力を指定する。 ※詳細後述 |
返り値 out
系列a, 系列vの畳み込み結果をnp.ndarrayとして返す。
サイズはモード毎に次のようになる。
- full: (N+M-1,)
- same: max(M, N)
- valid: max(M, N) - min(M, N) + 1
Note
N>Mを想定しているため、M>Nの場合は計算前にa,vが入れ替わる。
- サンプルコード
import numpy as np
a = [1,2,3,4,5]
v = [1,1,1]
np.convolve(a,v) #array([ 1, 3, 6, 9, 12, 9, 5])移動平均を計算する
ここでは例として、ノイズが足されたsin波に対して、np.convolveを用い移動平均を計算します。
移動平均を計算するためには、系列vを長さの逆数の系列にして、畳み込み演算します。
# ノイズを加えたsin波を生成
tt = np.linspace(0,1,100)*2*np.pi
xx = np.sin(tt)
a = xx + np.random.randn(100)*0.1
# 移動平均のサイズ
w_size = 7
v = np.ones(w_size) / w_size # 長さが7で,値が1/7の系列
out = np.convolve(a, v, mode='same')
# グラフ表示
fig, ax = plt.subplots()
ax.plot(tt, a, label='sin + noise')
ax.plot(tt, out,label='sin + noise (移動平均)')
ax.legend(fontsize=16, prop={"family":"AppleGothic"})
plt.show()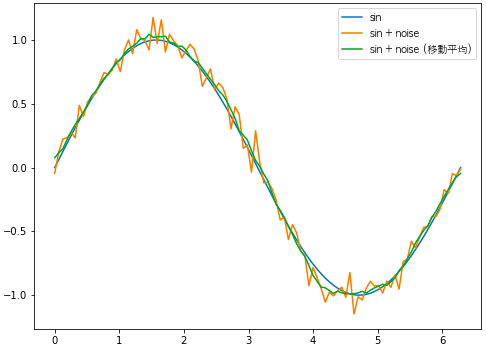
移動平均を行うことで、ノイズが低減されてsin波に近づいていることがわかります。
mode毎の出力の違い
np.convolveにはfull, valid, sameの3つのmodeがあるので、それぞれの動作の違いを見ていきます。
ここでは、aを長さN=5、値10の系列、vを長さM=3、値が1/3の系列としています。
N = 5
M = 3
a = np.ones(N)*10
v = np.ones(M) / M
# 移動平均を計算
out_full = np.convolve(a, v, mode='full') # array([ 3.33333333, 6.66666667, 10., 10., 10., 6.66666667, 3.33333333])
out_same = np.convolve(a, v, mode='same') # array([ 6.66666667, 10., 10., 10., 6.66666667])
out_valid = np.convolve(a, v, mode='valid') # array([10., 10., 10.])各modeの出力をグラフにしたのが次の図です。
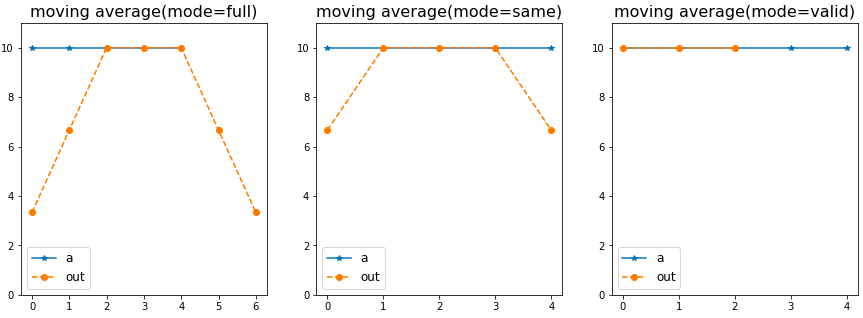
ここで、注目するポイントは出力(out)の長さと、両端の値です。
出力の長さは、mode毎に異なっており、fullが7(=N+M-1)で系列aより長く、sameが5(=max(M, N))で系列aと同じ、validが3(=max(M, N) - min(M, N)-1)で系列aより短くなっています。
両端の値は、full及びsameでは値が安定するまでの過渡応答が見られます。リファレンスではこれをBoundary Effect(境界の影響)と記載しています。
Boundary Effectは移動平均の用途によっては、問題になる場合がありますので、発生する原因と対応例についても後述します。
mode毎の特徴をまとめると次のようになります。
| full | same | valid | |
|---|---|---|---|
| 出力の長さ | N+M-1 | max(M, N) | max(M, N) - min(M, N)+1 |
| Boundary Effect | 有り | 有り | 無し |
参考までに、先ほどのグラフは以下のコードを実行することで表示できます。
n_data = 3 # 表示するデータ数
row=1 # 行数
col=3 # 列数
fig, ax = plt.subplots(nrows=row, ncols=col, figsize=(15,5))
ax[0].set_ylim(0, 11)
ax[0].set_title('moving average(mode=full)', fontsize=16)
ax[0].plot(range(len(a)), a, label='a')
ax[0].plot(range(len(out_full)), out_full, '--', label='out')
ax[0].legend(fontsize=12, loc=3)
ax[1].set_ylim(0, 11)
ax[1].set_title('moving average(mode=same)', fontsize=16)
ax[1].plot(range(len(a)), a, label='a')
ax[1].plot(range(len(out_same)), out_same, '--', label='out')
ax[1].legend(fontsize=12, loc=3)
ax[2].set_ylim(0, 11)
ax[2].set_title('moving average(mode=valid)', fontsize=16)
ax[2].plot(range(len(a)), a, label='a')
ax[2].plot(range(len(out_valid)), out_valid, '--', label='out')
ax[2].legend(fontsize=12, loc=3)mode毎の計算方法
mode毎に出力に違いがあることを見てきましたので、ここでは具体的な計算方法を確認します。それでは、mode=fullの計算から見ていきましょう。
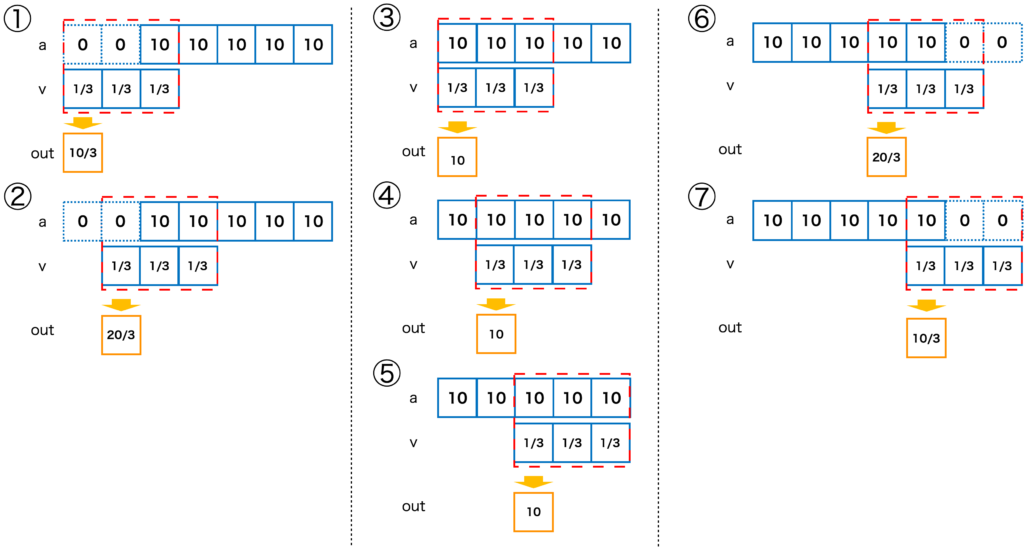
この図のように、①〜⑦の順に出力outが計算されます。
系列aに対して、系列bが横にスライドしながら結果を出力しているのが分かると思います。また、①〜②、⑥〜⑦では、系列aと系列bが部分的に重なるため、足りない部分は0で補間されます。
※移動平均の計算では系列bが全て同じ値なので分からないですが、実際は系列bは順番が反転されたものが、スライドしています。
次にmode=validの計算を確認します。
mode=valideでは、系列aと系列bが完全に重なっている範囲、図で言うと③〜⑤の出力が結果として得られます。両方の系列が完全に重なっている範囲のみ計算するため、Boudary Effectが現れません。
最後にmode=sameの計算を確認します。
sameの意味は、出力の長さが入力と一致することから名付けられています。mode=valideでは、長さがN-1短くなるのでその分が追加されます。図で言うと、mode=validの③〜⑤に加えて、②、⑥が追加になります。ちなみにNが偶数の場合、頭に1つ多く追加されます。
まとめると、
- mode=fullでは、系列aと系列vが部分的に一致している範囲も含めた結果が出力される。(図の①〜⑦)
- mode=validでは、系列aと系列vが完全に一致している範囲の結果が出力される。(図の③〜⑤)
- mode=sameでは、入力と同じ長さになるように結果が出力される。つまり、mode=validの両端にN-1だけ結果が追加される。(図の②〜⑥)
終わりに
np.convolveを使った移動平均の計算方法と、mode毎の結果の違いについて紹介しました。この記事の内容を理解すれば移動平均に限らず、重み付けした畳み込み演算も同様に利用できるかと思います。
この記事を読んで、もしかしたらBoundary Effectを無くして入力と同じ長さの出力を得るにはどうすれば良いか気になった方がいるかもしれません。
その場合は、入力系列aを補間(線形補間や、終端の値をコピーするなど)して、計算した出力から抜粋する方法などが考えられます。
この辺りも随時執筆していきたいと考えています。



コメント