機械学習を行う際、学習や予測に用いるデータの統計的性質は近しい方が学習効率や予測精度が良くなる傾向があります。この記事では、scikit-learnを用いた標準化及びスケーリングの実装方法を紹介します。
正規化/標準化/スケーリングという言葉は、サイトによって色んな意味で使われがちですので、初めに言葉の認識を合わせておきます。
- 標準化(Standardize)
- 分布の標準偏差が1になるようにデータを変換すること
- スケーリング(Scale)
- データが分布する範囲を変換すること。
分布の形状は変化しない。0〜1の範囲に変換することが多い。
- データが分布する範囲を変換すること。
- 正規化(Normalize)
- 標準化やスケーリングの両方を指していることが多い。曖昧さ回避のため本記事では用いない。
参考リンク: Scale, Standardize, or Normalize with Scikit-Learn
スケーリング
MinMaxScaler:
MinMaxScalerは、データを指定した範囲(デフォルトでは0〜1の範囲)に収まるようにスケーリングします。範囲が変換されるだけなので、分布rの形状は変わりません。また、スケーリングは列単位で実行されます。
from sklearn.preprocessing import MinMaxScaler
data = np.array([[1,2,3],
[4,5,6],
[7,8,9]])
scaler = MinMaxScaler()
scaler.fit(data)
scaler.transform(data)
# array([[0. , 0. , 0. ],
# [0.5, 0.5, 0.5],
# [1. , 1. , 1. ]])リファレンス: sklearn.preprocessing.MinMaxScaler
MinMaxScalerは直接データ全体への一括した適用や、1次元配列に対して適用することはできません。
もしデータ全体や、1次元配列への適用を行いたい場合は、reshapeを活用することで実現できます。
### データ全体へ適用
data = np.array([[1,2,3],
[4,5,6],
[7,8,9]])
data_one_column = data.reshape([-1,1])
scaler = MinMaxScaler()
scaled_data = scaler.fit_transform(data_one_column)
scaled_data.reshape(data.shape)
# array([[0. , 0.125, 0.25 ],
# [0.375, 0.5 , 0.625],
# [0.75 , 0.875, 1. ]])
### 1次元配列への適用
data = np.array([1,2,3,4,5]).reshape([-1,1])
print(data.shape)
# (5, 1)
scaler = MinMaxScaler()
scaler.fit_transform(data)
# array([[0. ],
# [0.25],
# [0.5 ],
# [0.75],
# [1. ]])参考: How to use MinMaxScaler on all columns?
参考: Python/sklearn - preprocessing.MinMaxScaler 1d deprecation
MaxAbsScaler
MaxAbsScalerは、各列毎のデータが [-1〜1]の範囲内に収まるようにスケーリングされます。
このスケーリングは列毎の絶対値の最大値で除算することで実現されます。
from sklearn.preprocessing import MaxAbsScaler
data = np.array([[5, 10, 3],
[0, 5, -6],
[-10, -1, -3]])
scaler = MaxAbsScaler()
scaler.fit_transform(data)
# array([[ 0.2, 1. , 0.5],
# [ 0. , 0.4, -1. ],
# [-1. , -0.1, -0.5]])リファレンス: sklearn.preprocessing.MaxAbsScaler
RobustScaler
RobustScalerは、中央値と四分位範囲を用いたスケーリングを行います。
元データに外れ値が含まれている場合、これまで紹介したスケーリング手法や、平均/分散を用いた標準化手法では上手く機能しないことがあります。そのような場合はRobustScalerを用いるとよりロバストな変換が可能です。
※四分位範囲とは、データを昇順にソートしデータ数で4等分した際に、中央にくる2つを合わせた範囲。4等分した際の区切りを四分位数と呼ぶ。
from sklearn.preprocessing import RobustScaler
data = np.array([[0, 0, 1],
[0, 0, 3],
[100, 10, 5],
[100, 10, 7],
[100, 100, 9]])
scaler = RobustScaler()
scaler.fit_transform(data)
# array([[-1. , -1. , -1. ],
# [-1. , -1. , -0.5],
# [ 0. , 0. , 0. ],
# [ 0. , 0. , 0.5],
# [ 0. , 9. , 1. ]])RobustScalerでは、データの中央値を減算し、四分位範囲で除算することでスケーリングします。そのためスケーリングの範囲は固定ではなくデータに依存します。
リファレンス: sklearn.preprocessing.RobustScaler
標準化
StandardScaler
StandardScalerは、データを平均0、分散1となるように標準化します。
数式で表現すると次の通りです。
$$z = \frac{x - u}{s}$$
ここで、$z$は変換後の値、$u$は平均、$s$は標準偏差です。
data = np.array([[2, 10, 3],
[0, 4, -6],
[-10, -1, -3]])
scaler = StandardScaler()
scaler.fit_transform(data)
# array([[ 0.88900089, 1.26012384, 1.33630621],
# [ 0.50800051, -0.07412493, -1.06904497],
# [-1.3970014 , -1.18599891, -0.26726124]])
0を中心とするように値が変換されているのが分かります。
非線形変換
ここまで紹介したスケーリングや標準化はデータの範囲を変換しますが、分布の形状は変化させない方法でした。記事の冒頭でも述べましたが、データの統計的性質は近いことで分析精度が上がることがあります。そこで、ここでは正規分布ではないデータを正規分布に近づける変換手法として、Box-Cox変換、Yeo-Johnson変換を紹介します。
Box-Cox変換
Box-Cox変換は、以下の式で表されます。
$x_{\lambda} = \begin{cases} \frac{x^{\lambda}-1}{\lambda} & {\rm if} \quad \lambda \neq 0 \\
\log x & {\rm if} \quad \lambda =0
\end{cases}
$
Box-Cox変換のポイントは、次の通りです。
- パラメータ$\lambda$が用意されており、scikit-learnでは特徴毎に歪度を小さくする$\lambda$が自動で選択される
- 正のデータにしか使用できない
- 負の値を含むデータを扱う場合は、絶対値を取った後に変換を行い、元の符号を付けるなどの工夫が必要
対数正規分布に従う乱数をBox-Cox変換した例を記載します。
from sklearn.preprocessing import PowerTransformer
data = np.random.lognormal(0, 1, 1000) # 対数正規分布に従う乱数
# Box-Cox変換
pt = PowerTransformer(method='box-cox', standardize=False)
box_cox = pt.fit_transform(data.reshape(-1,1))
# ヒストグラムで変換結果を確認
fig, ax = plt.subplots(1,2, figsize=(12,6))
fig.suptitle('Histogram', fontsize=24, color='black')
n_bins = 100
ax[0].hist(var, bins=n_bins, density=True) # density=Trueを追加すると確率密度になる。
ax[0].set_title('Lognormal')
ax[1].hist(box_cox, bins=n_bins, density=True)
ax[1].set_title('Box-Cox')
plt.show()リファレンス: sklearn.preprocessing.PowerTransformer
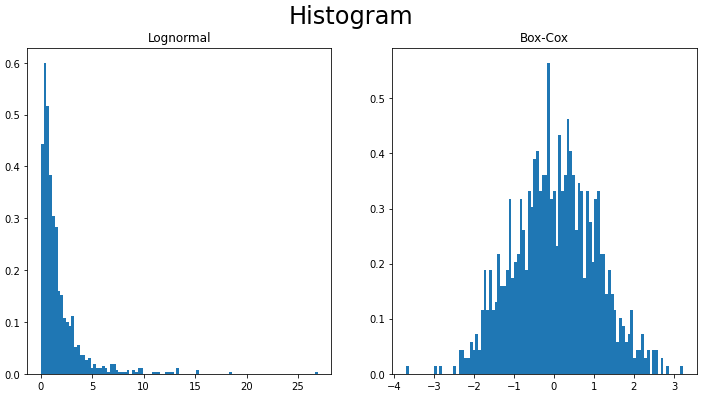
対数正規分布のデータ(左)に、Box-Cox変換を適用(右)することで、データの分布が正規分布に近づいていることが確認できます。
Yeo-Johnson変換
負の値を含むデータにも対応できるようにしたのが、Yeo-Johnson変換です。
Yeo-Johnson変換は次の式で表されます。一見複雑ですが、負の値を扱えるように場合分けが増えている以外はBox-Cox変換と非常に似ています。
$
x_{\lambda} =
\begin{cases}
[(x+1)^{\lambda}-1]/\lambda & {\rm if} \quad \lambda \neq 0, x \geq 0 \\
\ln(x+1) & {\rm if} \quad \lambda = 0, x \geq 0 \\
-[(-x+1)^{2 - \lambda}-1]/(2 - \lambda) & {\rm if} \quad \lambda \neq 2, x \lt 0 \\
-\ln(-x+1) & {\rm if} \quad \lambda = 2, x \lt 2 \\
\end{cases}
$
from sklearn.preprocessing import PowerTransformer
data = np.random.lognormal(0, 1, 1000) # 対数正規分布に従う乱数
# Yeo-Johnson変換
pt = PowerTransformer(method='yeo-johnson', standardize=False)
yeo_johnson = pt.fit_transform(data.reshape(-1,1))リファレンス: sklearn.preprocessing.PowerTransformer
まとめ
機械学習を行う際に欠かせない要素となる標準化や、スケーリングをPythonで実装する方法について紹介しました。各手法に向いているタスクやデータセットがあるので、やりたいことに合わせ各手法を選択できると良い思います。例えば、画像処理では0~255の範囲にスケーリングすることが多いのでMinMaxScalingを使う、外れ値の影響を低減したい場合はRobustScalerを使うなどです。
最後に、機械学習の精度向上する際のポイントがまとまっている書籍「Kaggleで勝つデータ分析の技術」を紹介したいと思います。この本では、日本を代表するようなTop Kagglerの方々がコンペで通用するデータ分析の手法を、コンペでの実績を踏まえて解説/紹介してくれています。この記事で紹介した標準化や、スケーリング以外にも様々な手法が紹介されているので、データ分析精度を向上させたい方は持っておいて損は1冊だと思います。
参考リンク
scikit-learn: 6.3.1. Standardization, or mean removal and variance scaling


コメント